OSCILLATORE SINUSOIDALE REALIZZATO
CON AMPLIFICATORE OPERAZIONALE
CIRCUITO RISONANTE LC E RETROAZIONE POSITIVA
Sulla base delle considerazioni e delle obiezioni fatte dagli amici della comunità di “Grix”, sul primo articolo, si è pensato di affrontare lo studio del nostro “oscillatore” secondo i canoni propri dell’elettronica.
Trattandosi, nello schema, di un nuovo circuito ci preoccuperemo:
- di verificare che per esso siano rispettate le condizioni di Barkhausen per i sistemi oscillanti;
- di, onde meglio comprendere la selettività del circuito, considerare il circuito LC come un filtro passa banda;
- di individuare, per i singoli componenti, dei range di variazione a garanzia di un buon funzionamento circuitale;
- di riportare i risultati dell’analisi sperimentale e con il simulatore Pspice;
- di riportare soltanto nel file allegato, le dimostrazioni matematiche.
Premesso che tutto quanto si può trovere nei “sacri testi” non sarà dimostrato procediamo:
Punto 1 – Criteri di Barkhausen
Considerato il seguente sistema retroazionato
Con A guadagno della linea diretta e β fattore di retroazione.
Affinchè un sistema retroazionato sia oscillante è necessario “sacri testi” siano verificate le seguenti condizioni:
Im[Aβ]=0 e Re[Aβ]=1
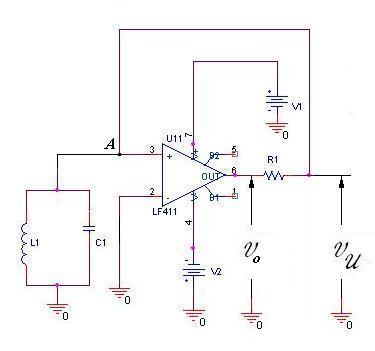
Consideriamo il nostro sistema nello schema più generale:
Supponiamo sia l’ A.O. ideale
Il circuito si può considerare come un Amplificatore Operazionale in configurazione non invertente con un segnale applicato al nodo A; segnale dato da:
per cui il circuito da analizzare, semplificato, diviene:
l’uscita sarà data da:
Verifichiamo i criteri di Barkhausen:
- il guadagno A è dato da:
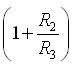
- il fattore di retroazione è dato da:
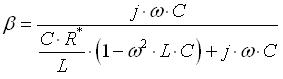
Im[Aβ]=0 quindi è come dire che l’argomento di Aβ sia nullo.
Affinchè ciò avvenga basta che la parte immaginaria del numero complesso β si annulli; per ottenere ciò basta che siano nulli o
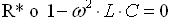
o entrambi.
Infatti con, anche una sola di queste condizioni, otteniamo:
dalla relazione
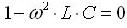
ricaviamo la frequenza d’oscillazione del sistema
Osserviamo che R*:
- sulla condizione di oscillazione non ha alcuna influenza;
- alla frequenza di oscillazione non ha neppure influenza sull’ampiezza del segnale di uscita.
Per non complicarci la vita e perché ridurre il numero dei componenti , quando si può fare è sempre salutare, la corto circuitiamo.
L’altra condizione da verificare è: Re[Aβ]=1 alla frequenza di oscillazione
quindi:
Sappiamo, che in pratica, affinchè s’inneschi l’oscillazione è necessario che
nulla ci vieta di fare R2 infinitamente grande, semplificando il circuito (meno componenti circuito più affidabile oltre che meno costoso), come di seguito indicato:
|
| clicca per ingrandire |
Avendo verificato le condizioni di Barkhausen possiamo asserire che il nostro è un sistema oscillante.
Punto 2- AZIONE FILTRANTE DEL PASSA BANDA LC
Premesso che essendoci una retroazione positiva l’uscita dell’A.O., se operiamo ad una frequenza sufficientemente più piccola della frequenza di taglio superiore dell’A.O, è certamente un’onda quadra:
- se indichiamo con la 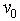 tensione massima all’uscita delld’A.O., detta onda quadra, secondo lo sviluppo in serie di Fourier, è data da:
tensione massima all’uscita delld’A.O., detta onda quadra, secondo lo sviluppo in serie di Fourier, è data da:
- il circuito LC si comporta come un filtro passa banda con frequenza di risonanza
l’impedenza del parallelo “LC” è data da:
possiamo asserire che alla frequenza di risonanza (che è anche la frequenza di oscillazione del nostro oscillatore) il filtro presenta una impedenza infinita ciò vuol dire che:
- la prima armonica si presenta identica a se stessa in uscita;
- le armoniche dalla terza in poi hanno ampiezza ridotta, per loro natura, e perché vengono attenuate dall’azione del filtro visto che la relativa frequenza di oscillazione è multipla di quella di risonanza;
Per quanto sopra, considerando l’A.O. come ideale, in uscita abbiamo la prima armonica dell’onda quadra che, sottolineamo ha un’ampiezza maggiore dell’onda quadra. Quanto sopra è:
a) coerente con quanto fornisce il simulatore Pspice;
b) non coerente con ciò che è stato rilevato sperimentalmente in quanto l’A.O. e il filtro LC sono reali e presentano delle resistenze elettriche che il modello ideale dei componenti trascura.
Approfondimento nel file PDF in allegato B
Punto 3- OSSERVAZIONI SUL VALORE DA ASSEGNARE AI COMPONENTI IL SISTEMA
Valore da assegnare ad R1
In questa analisi è necessario considerare l’A.O. come reale. Per le basse frequenza, o almeno fino alle frequenze ove si possono trascurare le reattanze di contatto e quelle distribuite, lo schema è il seguente:
si dimostra che il guadagno (vedi nel files PDF allegato A), considerato che
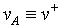
, è dato da;
ricaviamo l’influenza della resistenza R1 sul guadagno.
Osserviamo che il parallelo tra le resistenze Ri, R2 e R3 è più piccolo della più piccola delle tre, cioè di R3. Poniamo, in prima approssimazione, il parallelo pari ad R3; l’espressione del guadagno si semplifica come segue:
per quanto già osservato sui valori di R1 e R2, consideriamo i tre casi:
-
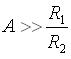 trascurando
trascurando 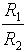 rispetto ad A ci resta:
rispetto ad A ci resta:
è facile rilevare che al crescere di R1 il guadagno diminuisce
- consideriamo (ipotesi esclusivamente teorica) il caso in cui
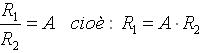 dalla:
dalla:
per cui possiamo asserire che R1, crescendo fino al valore sopra indicato fa sempre diminuire il guadagno.
- infine ( altra ipotesi teorica) consideriamo il caso in cui
l’espressione del guadagno diviene:
siccome al crescere di R1 il denominatore cresce più del numeratore e il guadagno diminuisce.
Concludendo poiché al crescere di R1 il guadagno diminuisce l’ampiezza del segnale di uscita diminuisce.
Evidenziamo che ciò si rileva nel circuito sperimentale in quanto nella simulazione con Pspice l’uscita ha l’ampiezza della prima armonica e non risente (entro certi limiti) della variazione di R1.
Parliamo di “certi limiti” perché al crescere di R1 l’oscillazione può non innescarsi a causa di un transitorio estremamente lungo. Ciò si può vedere dai risultati dell’analisi del transitorio (in file PDF dimostrazione in allegato B). Infatti, nella sua espressione, di seguito riportata, sipuò facilmente vedere come al crescere di R1 aumenti il tempo necessario
al relativo spegnimento.
A questo punto passiamo ad alcune osservazioni sugli ordini di grandezza delle resistenze in gioco. Così come riportano i “sacri testi”, se si volessero inserire, normalmente R
3 è dell'ordine di

mentre R
2 (ed R
L) sono dell'ordine di
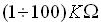
.
I valori più bassi sono utilizzati con i circuiti più veloci (dai MHz alle centinaia di MHz); i valori più alti sono tipici dei circuiti per frequenze minori (dalla continua alle centinaia di kHz).
La resistenza della sorgente del segnale, RS, di solito è un dato esterno, nel nostro caso si può assimilare alla resistenza del parallelo LC per cui si può ipotizzare, in prima approssomazione, pari a zero.
Punto 4- ANALISI SPERIMENTALE
Lanalisi, con simulatore Pspice e con circuito sperimentale, è stata sviluppata sul seguente circuito semplificato.
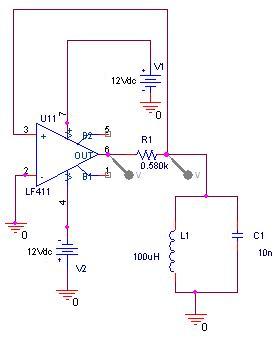 |
Componenti del circuito reale:
- 1 resistore da 470 Ω toll. 5%
- 1 condensatore poliestere 10 nF toll. 5% massima tensione applicabile 100 V;
- una induttanza da 100 micro Henry;
- un trimmer da 10KΩ;
- due condensatori poliestere da 100 nF
frequenza di risonanza
il valore sperimentale è di 125 KHz, vi è uno scarto di circa il 20%.
|
|
Circuito semplificato
|
|
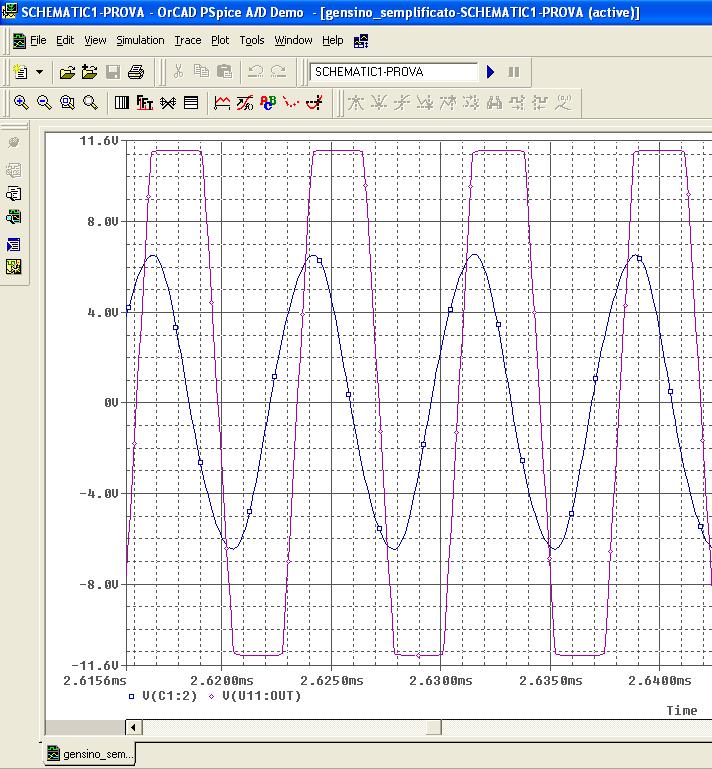 |
|
Uscita del circuito semplificato ottenuta con silulatore Pspice
|
|
L’analisi spettrale di Fourier fornisce
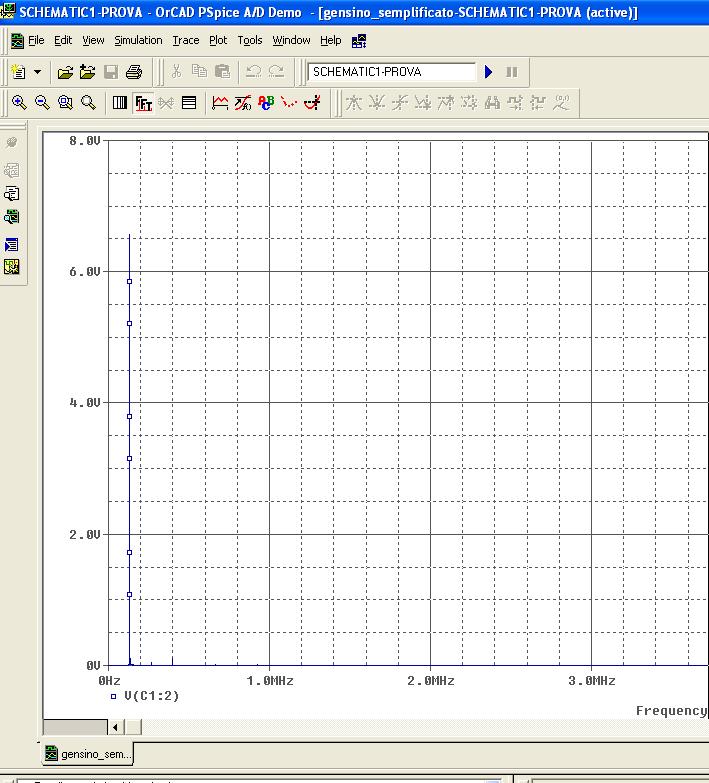 |
| |
|
Analisi spettrale, ottenuta con simulatore Pspice, del segnale presente ai capi del filtro LC. Si vede chiaramente che vi è un’armonica a circa 160 KHz; un’altra, di ampiezza molto piccola, a 200 KHz e prima di 1 MHz altre due di ampiezza quasi invisibile.
|
|
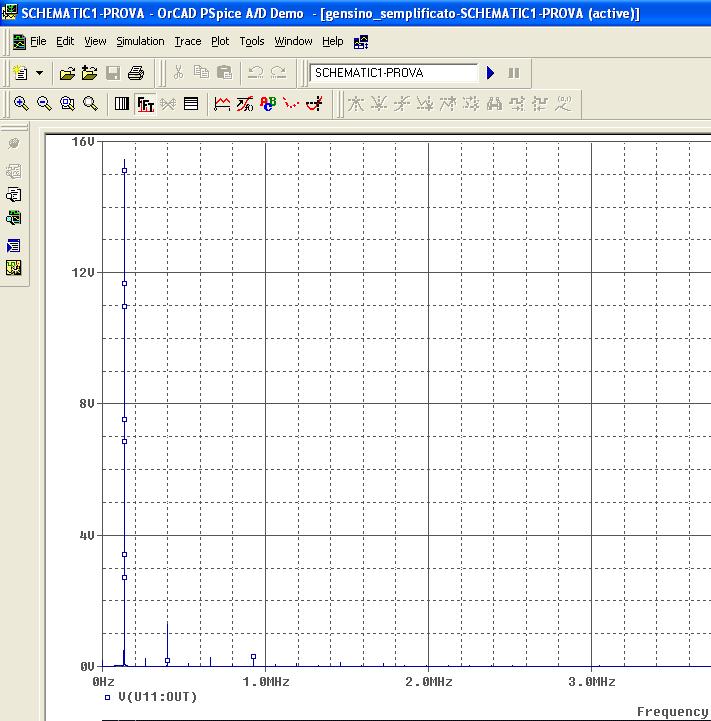 |
|
Analisi spettrale dell’onda presente all’uscita dell’A.O (onda quadra) ottenuta con simulatore Pspice. Possiamo vedere oltre alla prima armonica l’ ampiezza delle altre e così rilevare l’ottima azione filtrante di LC.
|
|
L’analisi sperimentale, sviluppata su circuito reale, ha fornito:
|
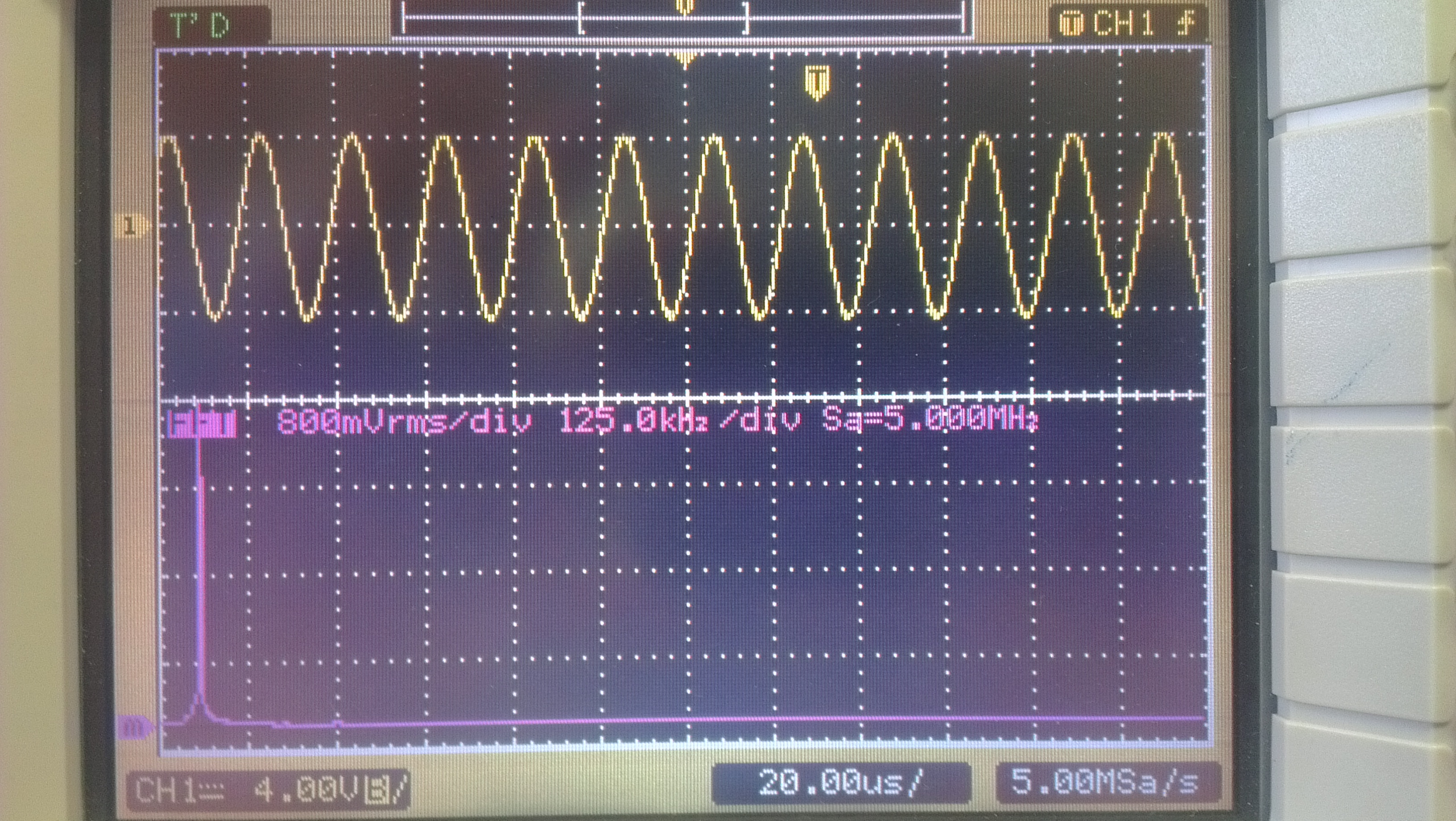
| | clicca per ingrandire |
|
|
Analisi spettrale dell’onda (sinusoidale) presente ai capi dell’LC. Come si può rilevare l’incidenza delle armoniche superiore alla prima è praticamente trascurabile. Evidenziamo che pur essendoci l’alimentazione a ±12 Volt la tensione di picco è 4 volt . Crediamo che ciò sia dovuto sia alla presenza di R1 che alla frequenza di taglio superiore dell’A.O.
|
| |
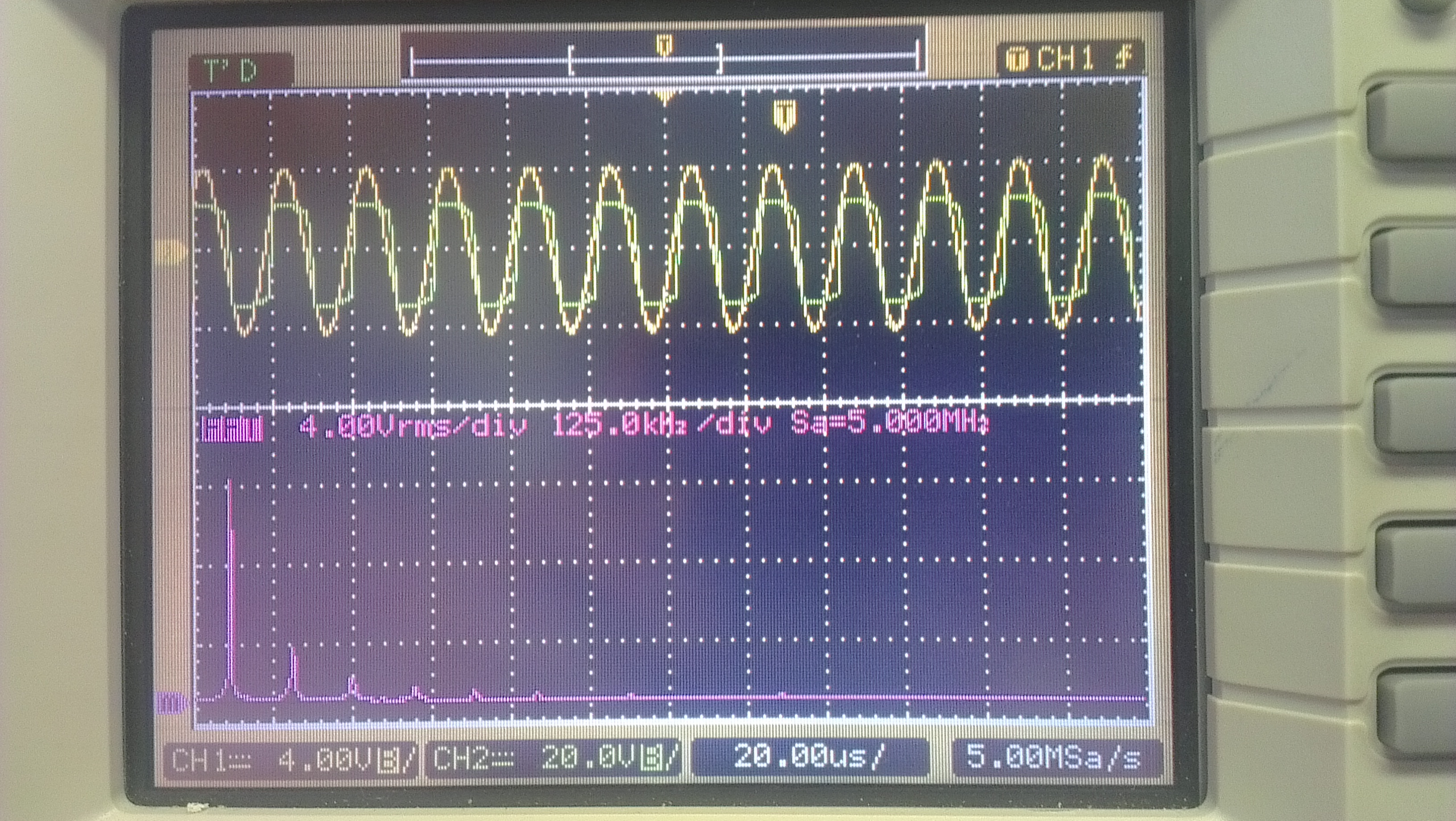
| | clicca per ingrandire |
|
|
Analisi spettrale dell’onda (quadra) presente all’uscita dell’A.O. Sono ben evidenti le armoniche superiori alla prima
|
|
|
| |
|
|
|
|
Il circuito sperimentale è il seguente
 |
Componenti, che ripetiamo per comodità:
- 1 resistore da 470 Ω toll. 5%
- 1 condensatore poliestere 10 nF toll. 5% massima tensione applicabile 100 V;
- una induttanza da 100 micro Henry;
- un trimmer da 10KΩ;
- due condensatori poliestere da 100 nF
frequenza di risonanza
il valore sperimentale è di 125 KHz vi è uno scarto di circa il 20%.
|
Altra prova sperimentale con valori diversi dei componenti circuitali
|
|
Componenti:
- 1 resistore da 470 Ω toll. 5%
- 1 condensatore poliestere 100 nF, tolleranza 10%, 63 Volt di esercizio ;
- una induttanza da 100 micro Henry;
- un trimmer da 10KΩ;
- due condensatori poliestere da 100 nF
- tensione di alimentazione dell’A.O. ±12 Volt.
frequenza di risonanza
il valore sperimentale è di 48,38KHz vi è uno scarto di circa il 3,8%.
|
|
Dall’immagine si rileva come abbiamo cercato di rendere i collegamenti più brevi possibili per non introdurre reattanze parassite.
|
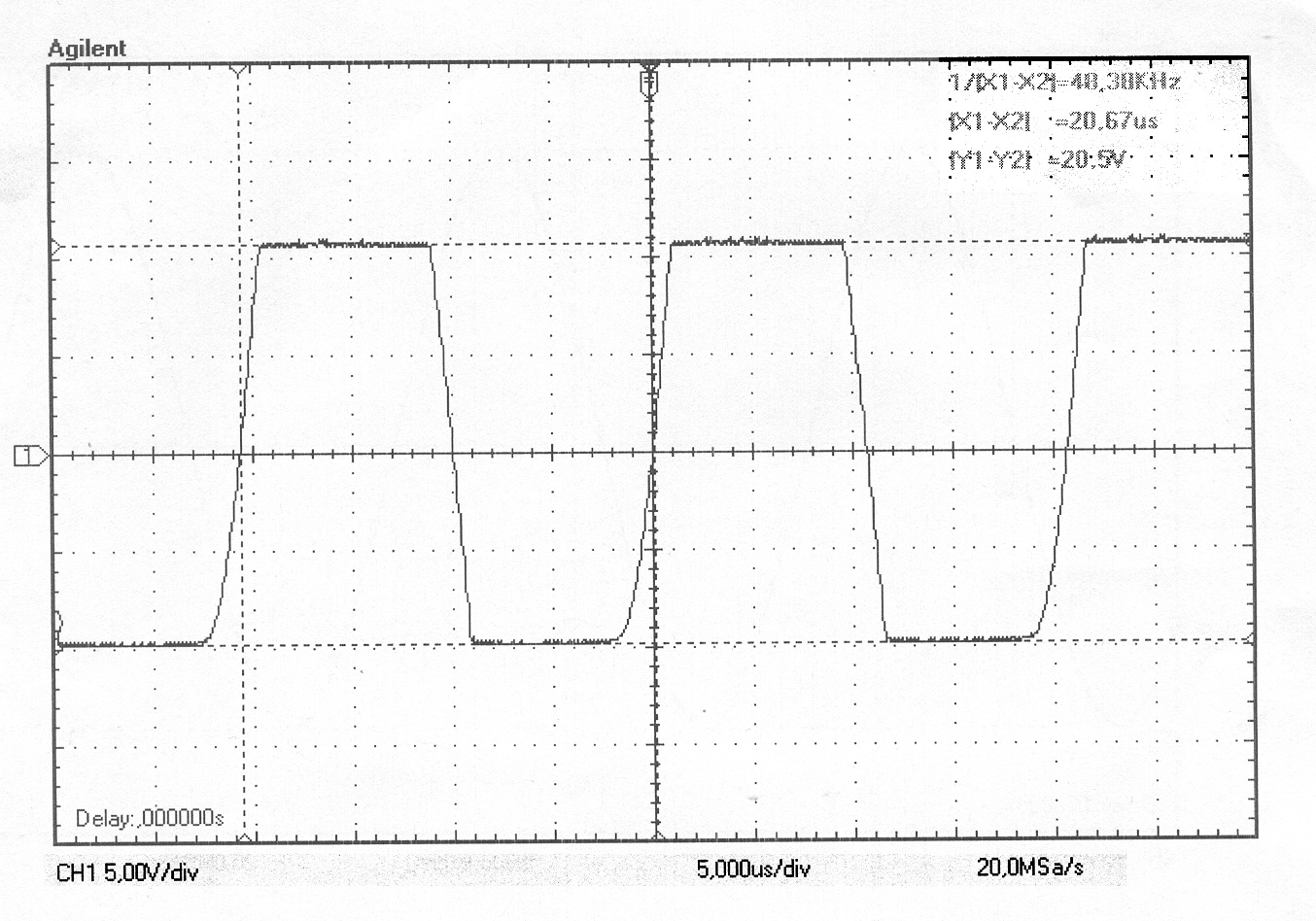
| | clicca per ingrandire |
|
|
Grafico ottenuto con trimmer posizionato a circa 2140 Ohm; sommando quindi la resistenza da 470 Ohm la R1è pari a 2610 Ohm. L'Onda quadra è accettabile. Tensione picco-picco dell’onda quadra pari a 20,5 Volt. Alimentazione ±12 Volt
|
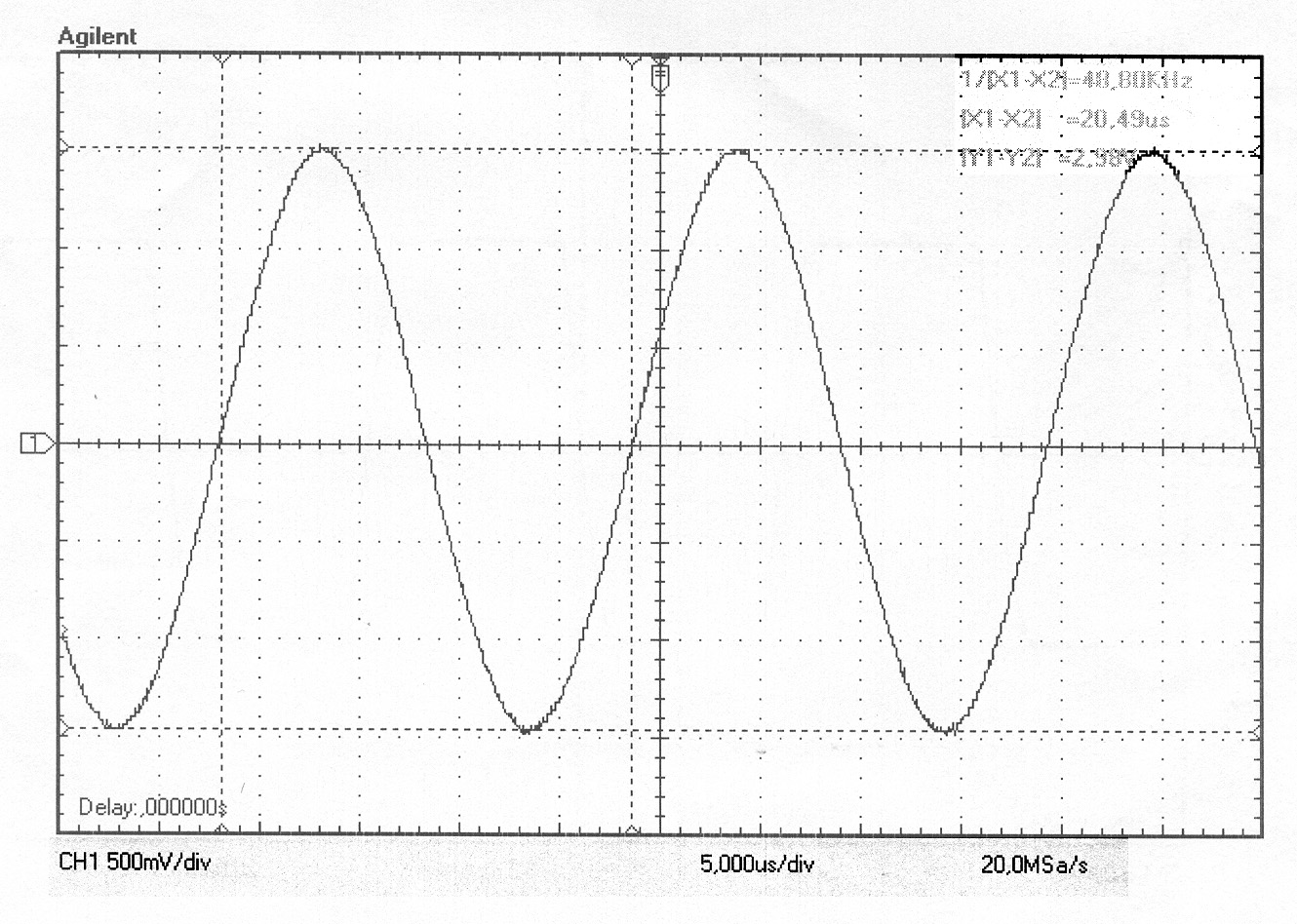
|
| clicca per ingrandire |
|
|
|
Tensione picco–picco dell’onda sinusoidale 2,98 Volt. L’onda è perfetta ma l’effetto della R1 si fa sentire sull'ampiezza del segnale.
|
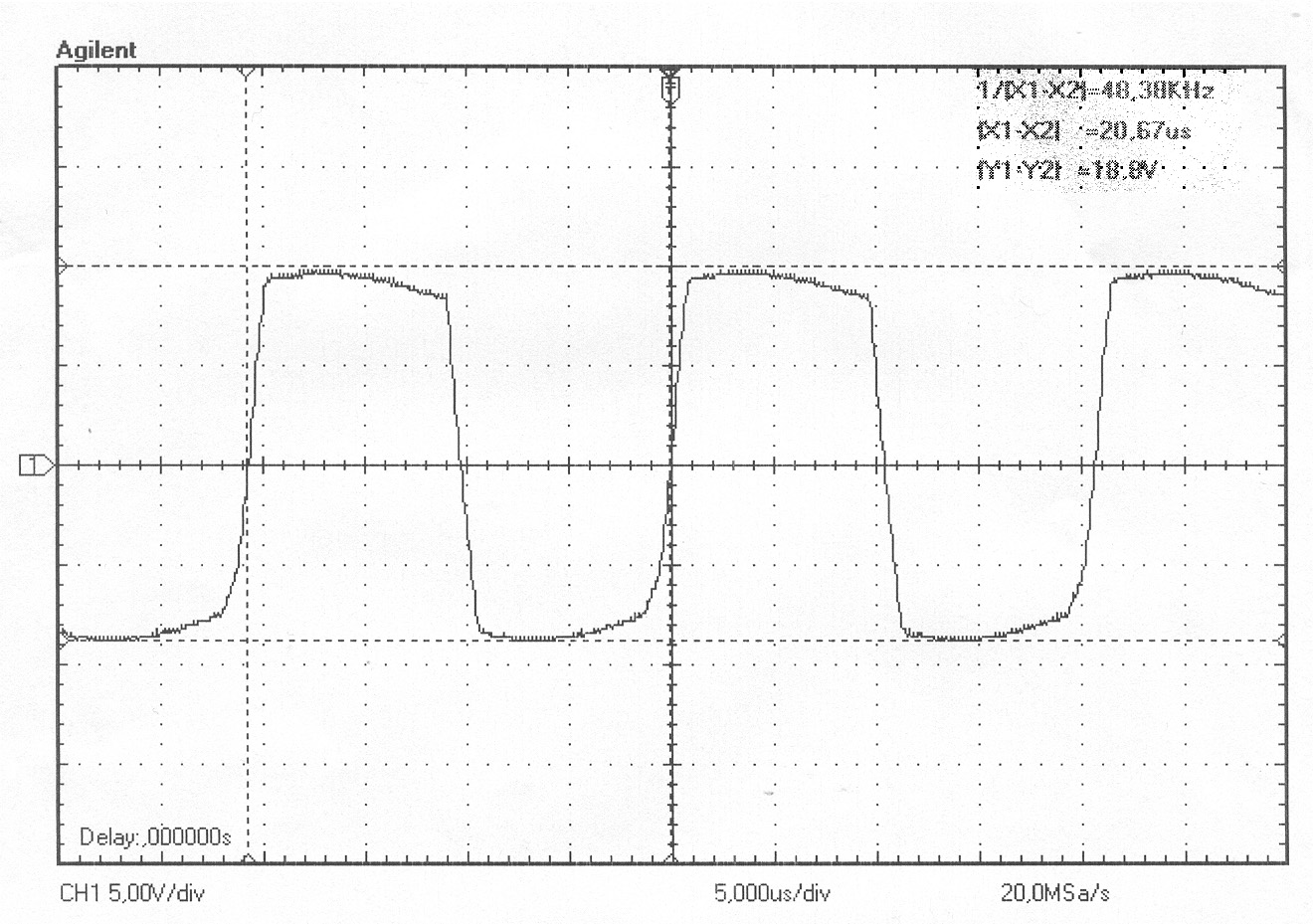
|
| clicca per ingrandire |
|
|
|
Resistenza R1 circa 580 Ohm, come si nota l’onda quadra risulta leggermente distorta e con tensione picco-picco pari a 18,8 Volt
Durante la sperimentazione si è rilevato che variando il trimmer (R1)da 600 Ohm a 1 Kohm l’oscillazione si innesca sempre.
|
Riportiamo, per valori dei componenti utilizzati nel circuito sperimentale, la simulazione con Pspice
|
|
|
Valore della resistenza R1 pari a 560 Ohm
Si può rilevare l’effetto retroattivo del segnale filtrato dal circuito risonante LC sull’onda quadra.
|
|
|
|
Valore della resistenza R1 pari a 2.6KOhm
Si evidenzia come al crescere della R 1 l’effetto retroattivo si fa sentire meno e l’onda quadra risulta meno distorta.
|
Conclusioni
In questa nuova analisi si è voluto tener conto dei suggerimenti che gli amici di “Grix” hanno fatto sulla stesura e sui contenuti del primo articolo.
Primo articolo che, precisiamo, non rinneghiamo perché in esso si era cercato di raccontare sia com’era nata l’idea del circuito sia spiegarne il funzionamento più fisicamente che con i canoni dell’elettronica.
L’oscillatore si presenta molto semplice da progettare, infatti:
- la frequenza di oscillazione è data da ;
- la resistenza di R1 deve rispettare la seguente condizione:
Si è visto che se è
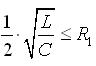
il transitorio è esponenziale decrescente altrimenti è oscillante decrescente. Valore dell’ordine del
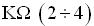
, riduce molto l’interazione tra onda quadra e sinusoidale, fornendo delle onde accettabili; di contro viene attenuata l’ampiezza dell’onda sinusoidale.
Disponibili sempre ad ogni chiarimento e ad ogni correzione, chiediamo agli amici di “Grix” di, se vogliono, provare il circuito perché “è lui l’oggetto in discussione” non noi.
E poiché prima, questo bello e semplice circuitino (concedetecelo) non c’era e adesso esiste ed è nato in Italia, non ci dispiacerebbe se volessero suggerire un nome che……suoni tutto italiano.
Grazie per l’attenzione.
 OSCILLATORE SINUSOIDALE A RETROAZIONE POSITIVA.pdf
OSCILLATORE SINUSOIDALE A RETROAZIONE POSITIVA.pdf
emmstudio